Optimization
The evening’s the best part of the day. You’ve done your day’s work. Now you can put your feet up and enjoy it.
Kazuo Ishiguro, The Remains of the Day
If I still lived in New Orleans, I’d call this chapter a lagniappe, a little something extra given for free to a customer. You’ve got a whole book and a complete virtual machine already, but I want you to have some more fun hacking on clox. This time, we’re going for pure performance. We’ll apply two very different optimizations to our virtual machine. In the process, you’ll get a feel for measuring and improving the performance of a language implementation—or any program, really.
30 . 1Measuring Performance
Optimization means taking a working application and improving its performance. An optimized program does the same thing, it just takes less resources to do so. The resource we usually think of when optimizing is runtime speed, but it can also be important to reduce memory usage, startup time, persistent storage size, or network bandwidth. All physical resources have some cost—even if the cost is mostly in wasted human time—so optimization work often pays off.
There was a time in the early days of computing that a skilled programmer could hold the entire hardware architecture and compiler pipeline in their head and understand a program’s performance just by thinking real hard. Those days are long gone, separated from the present by microcode, cache lines, branch prediction, deep compiler pipelines, and mammoth instruction sets. We like to pretend C is a “low-level” language, but the stack of technology between
printf("Hello, world!");
and a greeting appearing on screen is now perilously tall.
Optimization today is an empirical science. Our program is a border collie sprinting through the hardware’s obstacle course. If we want her to reach the end faster, we can’t just sit and ruminate on canine physiology until enlightenment strikes. Instead, we need to observe her performance, see where she stumbles, and then find faster paths for her to take.
Much like agility training is particular to one dog and one obstacle course, we can’t assume that our virtual machine optimizations will make all Lox programs run faster on all hardware. Different Lox programs stress different areas of the VM, and different architectures have their own strengths and weaknesses.
30 . 1 . 1Benchmarks
When we add new functionality, we validate correctness by writing tests—Lox programs that use a feature and validate the VM’s behavior. Tests pin down semantics and ensure we don’t break existing features when we add new ones. We have similar needs when it comes to performance:
-
How do we validate that an optimization does improve performance, and by how much?
-
How do we ensure that other unrelated changes don’t regress performance?
The Lox programs we write to accomplish those goals are benchmarks. These are carefully crafted programs that stress some part of the language implementation. They measure not what the program does, but how long it takes to do it.
By measuring the performance of a benchmark before and after a change, you can see what your change does. When you land an optimization, all of the tests should behave exactly the same as they did before, but hopefully the benchmarks run faster.
Once you have an entire suite of benchmarks, you can measure not just that an optimization changes performance, but on which kinds of code. Often you’ll find that some benchmarks get faster while others get slower. Then you have to make hard decisions about what kinds of code your language implementation optimizes for.
The suite of benchmarks you choose to write is a key part of that decision. In the same way that your tests encode your choices around what correct behavior looks like, your benchmarks are the embodiment of your priorities when it comes to performance. They will guide which optimizations you implement, so choose your benchmarks carefully, and don’t forget to periodically reflect on whether they are helping you reach your larger goals.
Benchmarking is a subtle art. Like tests, you need to balance not overfitting to your implementation while ensuring that the benchmark does actually tickle the code paths that you care about. When you measure performance, you need to compensate for variance caused by CPU throttling, caching, and other weird hardware and operating system quirks. I won’t give you a whole sermon here, but treat benchmarking as its own skill that improves with practice.
30 . 1 . 2Profiling
OK, so you’ve got a few benchmarks now. You want to make them go faster. Now what? First of all, let’s assume you’ve done all the obvious, easy work. You are using the right algorithms and data structures—or, at least, you aren’t using ones that are aggressively wrong. I don’t consider using a hash table instead of a linear search through a huge unsorted array “optimization” so much as “good software engineering”.
Since the hardware is too complex to reason about our program’s performance from first principles, we have to go out into the field. That means profiling. A profiler, if you’ve never used one, is a tool that runs your program and tracks hardware resource use as the code executes. Simple ones show you how much time was spent in each function in your program. Sophisticated ones log data cache misses, instruction cache misses, branch mispredictions, memory allocations, and all sorts of other metrics.
There are many profilers out there for various operating systems and languages. On whatever platform you program, it’s worth getting familiar with a decent profiler. You don’t need to be a master. I have learned things within minutes of throwing a program at a profiler that would have taken me days to discover on my own through trial and error. Profilers are wonderful, magical tools.
30 . 2Faster Hash Table Probing
Enough pontificating, let’s get some performance charts going up and to the right. The first optimization we’ll do, it turns out, is about the tiniest possible change we could make to our VM.
When I first got the bytecode virtual machine that clox is descended from working, I did what any self-respecting VM hacker would do. I cobbled together a couple of benchmarks, fired up a profiler, and ran those scripts through my interpreter. In a dynamically typed language like Lox, a large fraction of user code is field accesses and method calls, so one of my benchmarks looked something like this:
class Zoo { init() { this.aardvark = 1; this.baboon = 1; this.cat = 1; this.donkey = 1; this.elephant = 1; this.fox = 1; } ant() { return this.aardvark; } banana() { return this.baboon; } tuna() { return this.cat; } hay() { return this.donkey; } grass() { return this.elephant; } mouse() { return this.fox; } } var zoo = Zoo(); var sum = 0; var start = clock(); while (sum < 100000000) { sum = sum + zoo.ant() + zoo.banana() + zoo.tuna() + zoo.hay() + zoo.grass() + zoo.mouse(); } print clock() - start; print sum;
If you’ve never seen a benchmark before, this might seem ludicrous. What is going on here? The program itself doesn’t intend to do anything useful. What it does do is call a bunch of methods and access a bunch of fields since those are the parts of the language we’re interested in. Fields and methods live in hash tables, so it takes care to populate at least a few interesting keys in those tables. That is all wrapped in a big loop to ensure our profiler has enough execution time to dig in and see where the cycles are going.
Before I tell you what my profiler showed me, spend a minute taking a few guesses. Where in clox’s codebase do you think the VM spent most of its time? Is there any code we’ve written in previous chapters that you suspect is particularly slow?
Here’s what I found: Naturally, the function with the greatest inclusive time is
run(). (Inclusive time means the total time spent in some function and all
other functions it calls—the total time between when you enter the function
and when it returns.) Since run() is the main bytecode execution loop, it
drives everything.
Inside run(), there are small chunks of time sprinkled in various cases in the
bytecode switch for common instructions like OP_POP, OP_RETURN, and
OP_ADD. The big heavy instructions are OP_GET_GLOBAL with 17% of the
execution time, OP_GET_PROPERTY at 12%, and OP_INVOKE which takes a whopping
42% of the total running time.
So we’ve got three hotspots to optimize? Actually, no. Because it turns out
those three instructions spend almost all of their time inside calls to the same
function: tableGet(). That function claims a whole 72% of the execution time
(again, inclusive). Now, in a dynamically typed language, we expect to spend a
fair bit of time looking stuff up in hash tables—it’s sort of the price of
dynamism. But, still, wow.
30 . 2 . 1Slow key wrapping
If you take a look at tableGet(), you’ll see it’s mostly a wrapper around a
call to findEntry() where the actual hash table lookup happens. To refresh
your memory, here it is in full:
static Entry* findEntry(Entry* entries, int capacity, ObjString* key) { uint32_t index = key->hash % capacity; Entry* tombstone = NULL; for (;;) { Entry* entry = &entries[index]; if (entry->key == NULL) { if (IS_NIL(entry->value)) { // Empty entry. return tombstone != NULL ? tombstone : entry; } else { // We found a tombstone. if (tombstone == NULL) tombstone = entry; } } else if (entry->key == key) { // We found the key. return entry; } index = (index + 1) % capacity; } }
When running that previous benchmark—on my machine, at least—the VM spends 70% of the total execution time on one line in this function. Any guesses as to which one? No? It’s this:
uint32_t index = key->hash % capacity;
That pointer dereference isn’t the problem. It’s the little %. It turns out
the modulo operator is really slow. Much slower than other arithmetic operators. Can we do something better?
In the general case, it’s really hard to re-implement a fundamental arithmetic operator in user code in a way that’s faster than what the CPU itself can do. After all, our C code ultimately compiles down to the CPU’s own arithmetic operations. If there were tricks we could use to go faster, the chip would already be using them.
However, we can take advantage of the fact that we know more about our problem than the CPU does. We use modulo here to take a key string’s hash code and wrap it to fit within the bounds of the table’s entry array. That array starts out at eight elements and grows by a factor of two each time. We know—and the CPU and C compiler do not—that our table’s size is always a power of two.
Because we’re clever bit twiddlers, we know a faster way to calculate the remainder of a number modulo a power of two: bit masking. Let’s say we want to calculate 229 modulo 64. The answer is 37, which is not particularly apparent in decimal, but is clearer when you view those numbers in binary:
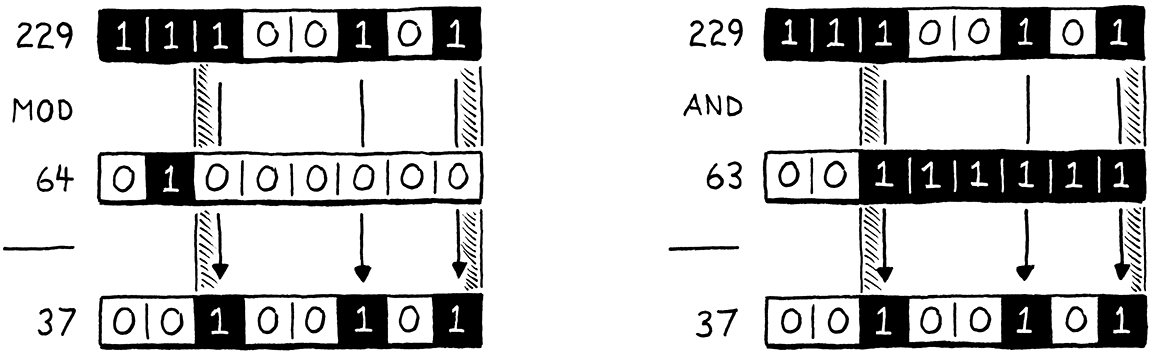
On the left side of the illustration, notice how the result (37) is simply the dividend (229) with the highest two bits shaved off? Those two highest bits are the bits at or to the left of the divisor’s single 1 bit.
On the right side, we get the same result by taking 229 and bitwise AND-ing it with 63, which is one less than our original power of two divisor. Subtracting one from a power of two gives you a series of 1 bits. That is exactly the mask we need in order to strip out those two leftmost bits.
In other words, you can calculate a number modulo any power of two by simply AND-ing it with that power of two minus one. I’m not enough of a mathematician to prove to you that this works, but if you think it through, it should make sense. We can replace that slow modulo operator with a very fast decrement and bitwise AND. We simply change the offending line of code to this:
static Entry* findEntry(Entry* entries, int capacity,
ObjString* key) {
in findEntry()
replace 1 line
uint32_t index = key->hash & (capacity - 1);
Entry* tombstone = NULL;
CPUs love bitwise operators, so it’s hard to improve on that.
Our linear probing search may need to wrap around the end of the array, so there
is another modulo in findEntry() to update.
// We found the key.
return entry;
}
in findEntry()
replace 1 line
index = (index + 1) & (capacity - 1);
}
This line didn’t show up in the profiler since most searches don’t wrap.
The findEntry() function has a sister function, tableFindString() that does
a hash table lookup for interning strings. We may as well apply the same
optimizations there too. This function is called only when interning strings,
which wasn’t heavily stressed by our benchmark. But a Lox program that created
lots of strings might noticeably benefit from this change.
if (table->count == 0) return NULL;
in tableFindString()
replace 1 line
uint32_t index = hash & (table->capacity - 1);
for (;;) {
Entry* entry = &table->entries[index];
And also when the linear probing wraps around.
return entry->key;
}
in tableFindString()
replace 1 line
index = (index + 1) & (table->capacity - 1);
}
Let’s see if our fixes were worth it. I tweaked that zoological benchmark to count how many batches of 10,000 calls it can run in ten seconds. More batches equals faster performance. On my machine using the unoptimized code, the benchmark gets through 3,192 batches. After this optimization, that jumps to 6,249.
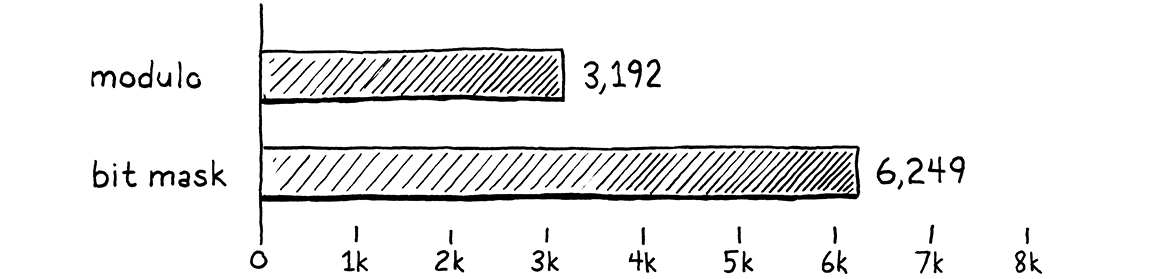
That’s almost exactly twice as much work in the same amount of time. We made the VM twice as fast (usual caveat: on this benchmark). That is a massive win when it comes to optimization. Usually you feel good if you can claw a few percentage points here or there. Since methods, fields, and global variables are so prevalent in Lox programs, this tiny optimization improves performance across the board. Almost every Lox program benefits.
Now, the point of this section is not that the modulo operator is profoundly evil and you should stamp it out of every program you ever write. Nor is it that micro-optimization is a vital engineering skill. It’s rare that a performance problem has such a narrow, effective solution. We got lucky.
The point is that we didn’t know that the modulo operator was a performance drain until our profiler told us so. If we had wandered around our VM’s codebase blindly guessing at hotspots, we likely wouldn’t have noticed it. What I want you to take away from this is how important it is to have a profiler in your toolbox.
To reinforce that point, let’s go ahead and run the original benchmark in our
now-optimized VM and see what the profiler shows us. On my machine, tableGet()
is still a fairly large chunk of execution time. That’s to be expected for a
dynamically typed language. But it has dropped from 72% of the total execution
time down to 35%. That’s much more in line with what we’d like to see and shows
that our optimization didn’t just make the program faster, but made it faster
in the way we expected. Profilers are as useful for verifying solutions as
they are for discovering problems.
30 . 3NaN Boxing
This next optimization has a very different feel. Thankfully, despite the odd name, it does not involve punching your grandmother. It’s different, but not, like, that different. With our previous optimization, the profiler told us where the problem was, and we merely had to use some ingenuity to come up with a solution.
This optimization is more subtle, and its performance effects more scattered across the virtual machine. The profiler won’t help us come up with this. Instead, it was invented by someone thinking deeply about the lowest levels of machine architecture.
Like the heading says, this optimization is called NaN boxing or sometimes NaN tagging. Personally I like the latter name because “boxing” tends to imply some kind of heap-allocated representation, but the former seems to be the more widely used term. This technique changes how we represent values in the VM.
On a 64-bit machine, our Value type takes up 16 bytes. The struct has two fields, a type tag and a union for the payload. The largest fields in the union are an Obj pointer and a double, which are both 8 bytes. To keep the union field aligned to an 8-byte boundary, the compiler adds padding after the tag too:

That’s pretty big. If we could cut that down, then the VM could pack more values into the same amount of memory. Most computers have plenty of RAM these days, so the direct memory savings aren’t a huge deal. But a smaller representation means more Values fit in a cache line. That means fewer cache misses, which affects speed.
If Values need to be aligned to their largest payload size, and a Lox number or Obj pointer needs a full 8 bytes, how can we get any smaller? In a dynamically typed language like Lox, each value needs to carry not just its payload, but enough additional information to determine the value’s type at runtime. If a Lox number is already using the full 8 bytes, where could we squirrel away a couple of extra bits to tell the runtime “this is a number”?
This is one of the perennial problems for dynamic language hackers. It particularly bugs them because statically typed languages don’t generally have this problem. The type of each value is known at compile time, so no extra memory is needed at runtime to track it. When your C compiler compiles a 32-bit int, the resulting variable gets exactly 32 bits of storage.
Dynamic language folks hate losing ground to the static camp, so they’ve come up with a number of very clever ways to pack type information and a payload into a small number of bits. NaN boxing is one of those. It’s a particularly good fit for languages like JavaScript and Lua, where all numbers are double-precision floating point. Lox is in that same boat.
30 . 3 . 1What is (and is not) a number?
Before we start optimizing, we need to really understand how our friend the CPU represents floating-point numbers. Almost all machines today use the same scheme, encoded in the venerable scroll IEEE 754, known to mortals as the “IEEE Standard for Floating-Point Arithmetic”.
In the eyes of your computer, a 64-bit, double-precision, IEEE floating-point number looks like this:

-
Starting from the right, the first 52 bits are the fraction, mantissa, or significand bits. They represent the significant digits of the number, as a binary integer.
-
Next to that are 11 exponent bits. These tell you how far the mantissa is shifted away from the decimal (well, binary) point.
-
The highest bit is the sign bit, which indicates whether the number is positive or negative.
I know that’s a little vague, but this chapter isn’t a deep dive on floating point representation. If you want to know how the exponent and mantissa play together, there are already better explanations out there than I could write.
The important part for our purposes is that the spec carves out a special case exponent. When all of the exponent bits are set, then instead of just representing a really big number, the value has a different meaning. These values are “Not a Number” (hence, NaN) values. They represent concepts like infinity or the result of division by zero.
Any double whose exponent bits are all set is a NaN, regardless of the mantissa bits. That means there’s lots and lots of different NaN bit patterns. IEEE 754 divides those into two categories. Values where the highest mantissa bit is 0 are called signalling NaNs, and the others are quiet NaNs. Signalling NaNs are intended to be the result of erroneous computations, like division by zero. A chip may detect when one of these values is produced and abort a program completely. They may self-destruct if you try to read one.
Quiet NaNs are supposed to be safer to use. They don’t represent useful numeric values, but they should at least not set your hand on fire if you touch them.
Every double with all of its exponent bits set and its highest mantissa bit set is a quiet NaN. That leaves 52 bits unaccounted for. We’ll avoid one of those so that we don’t step on Intel’s “QNaN Floating-Point Indefinite” value, leaving us 51 bits. Those remaining bits can be anything. We’re talking 2,251,799,813,685,248 unique quiet NaN bit patterns.
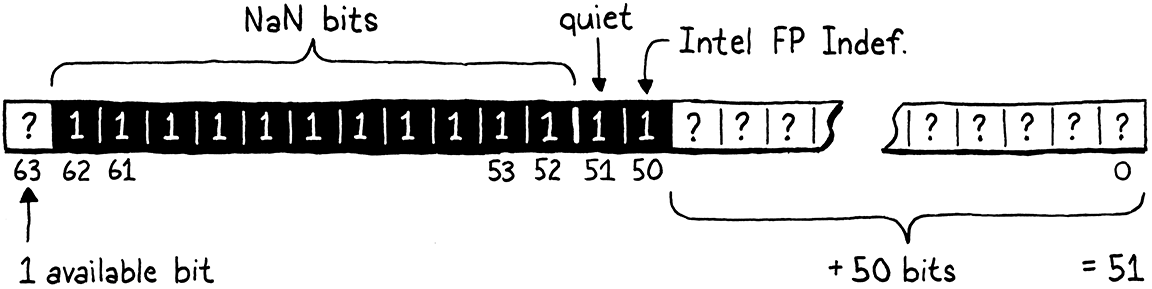
This means a 64-bit double has enough room to store all of the various different
numeric floating-point values and also has room for another 51 bits of data
that we can use however we want. That’s plenty of room to set aside a couple of
bit patterns to represent Lox’s nil, true, and false values. But what
about Obj pointers? Don’t pointers need a full 64 bits too?
Fortunately, we have another trick up our other sleeve. Yes, technically pointers on a 64-bit architecture are 64 bits. But, no architecture I know of actually uses that entire address space. Instead, most widely used chips today only ever use the low 48 bits. The remaining 16 bits are either unspecified or always zero.
If we’ve got 51 bits, we can stuff a 48-bit pointer in there with three bits to
spare. Those three bits are just enough to store tiny type tags to distinguish
between nil, Booleans, and Obj pointers.
That’s NaN boxing. Within a single 64-bit double, you can store all of the different floating-point numeric values, a pointer, or any of a couple of other special sentinel values. Half the memory usage of our current Value struct, while retaining all of the fidelity.
What’s particularly nice about this representation is that there is no need to convert a numeric double value into a “boxed” form. Lox numbers are just normal, 64-bit doubles. We still need to check their type before we use them, since Lox is dynamically typed, but we don’t need to do any bit shifting or pointer indirection to go from “value” to “number”.
For the other value types, there is a conversion step, of course. But, fortunately, our VM hides all of the mechanism to go from values to raw types behind a handful of macros. Rewrite those to implement NaN boxing, and the rest of the VM should just work.
30 . 3 . 2Conditional support
I know the details of this new representation aren’t clear in your head yet. Don’t worry, they will crystallize as we work through the implementation. Before we get to that, we’re going to put some compile-time scaffolding in place.
For our previous optimization, we rewrote the previous slow code and called it done. This one is a little different. NaN boxing relies on some very low-level details of how a chip represents floating-point numbers and pointers. It probably works on most CPUs you’re likely to encounter, but you can never be totally sure.
It would suck if our VM completely lost support for an architecture just because of its value representation. To avoid that, we’ll maintain support for both the old tagged union implementation of Value and the new NaN-boxed form. We select which representation we want at compile time using this flag:
#include <stdint.h>
#define NAN_BOXING
#define DEBUG_PRINT_CODE
If that’s defined, the VM uses the new form. Otherwise, it reverts to the old style. The few pieces of code that care about the details of the value representation—mainly the handful of macros for wrapping and unwrapping Values—vary based on whether this flag is set. The rest of the VM can continue along its merry way.
Most of the work happens in the “value” module where we add a section for the new type.
typedef struct ObjString ObjString;
#ifdef NAN_BOXING typedef uint64_t Value; #else
typedef enum {
When NaN boxing is enabled, the actual type of a Value is a flat, unsigned 64-bit integer. We could use double instead, which would make the macros for dealing with Lox numbers a little simpler. But all of the other macros need to do bitwise operations and uint64_t is a much friendlier type for that. Outside of this module, the rest of the VM doesn’t really care one way or the other.
Before we start re-implementing those macros, we close the #else branch of the
#ifdef at the end of the definitions for the old representation.
#define OBJ_VAL(object) ((Value){VAL_OBJ, {.obj = (Obj*)object}})
#endif
typedef struct {
Our remaining task is simply to fill in that first #ifdef section with new
implementations of all the stuff already in the #else side. We’ll work through
it one value type at a time, from easiest to hardest.
30 . 3 . 3Numbers
We’ll start with numbers since they have the most direct representation under NaN boxing. To “convert” a C double to a NaN-boxed clox Value, we don’t need to touch a single bit—the representation is exactly the same. But we do need to convince our C compiler of that fact, which we made harder by defining Value to be uint64_t.
We need to get the compiler to take a set of bits that it thinks are a double and use those same bits as a uint64_t, or vice versa. This is called type punning. C and C++ programmers have been doing this since the days of bell bottoms and 8-tracks, but the language specifications have hesitated to say which of the many ways to do this is officially sanctioned.
I know one way to convert a double to Value and back that I believe is
supported by both the C and C++ specs. Unfortunately, it doesn’t fit in a single
expression, so the conversion macros have to call out to helper functions.
Here’s the first macro:
typedef uint64_t Value;
#define NUMBER_VAL(num) numToValue(num)
#else
That macro passes the double here:
#define NUMBER_VAL(num) numToValue(num)
static inline Value numToValue(double num) { Value value; memcpy(&value, &num, sizeof(double)); return value; }
#else
I know, weird, right? The way to treat a series of bytes as having a different
type without changing their value at all is memcpy()? This looks horrendously
slow: Create a local variable. Pass its address to the operating system through
a syscall to copy a few bytes. Then return the result, which is the exact same
bytes as the input. Thankfully, because this is the supported idiom for type
punning, most compilers recognize the pattern and optimize away the memcpy()
entirely.
“Unwrapping” a Lox number is the mirror image.
typedef uint64_t Value;
#define AS_NUMBER(value) valueToNum(value)
#define NUMBER_VAL(num) numToValue(num)
That macro calls this function:
#define NUMBER_VAL(num) numToValue(num)
static inline double valueToNum(Value value) { double num; memcpy(&num, &value, sizeof(Value)); return num; }
static inline Value numToValue(double num) {
It works exactly the same except we swap the types. Again, the compiler will
eliminate all of it. Even though those calls to
memcpy() will disappear, we still need to show the compiler which memcpy()
we’re calling so we also need an include.
#define clox_value_h
#include <string.h>
#include "common.h"
That was a lot of code to ultimately do nothing but silence the C type checker. Doing a runtime type test on a Lox number is a little more interesting. If all we have are exactly the bits for a double, how do we tell that it is a double? It’s time to get bit twiddling.
typedef uint64_t Value;
#define IS_NUMBER(value) (((value) & QNAN) != QNAN)
#define AS_NUMBER(value) valueToNum(value)
We know that every Value that is not a number will use a special quiet NaN representation. And we presume we have correctly avoided any of the meaningful NaN representations that may actually be produced by doing arithmetic on numbers.
If the double has all of its NaN bits set, and the quiet NaN bit set, and one more for good measure, we can be pretty certain it is one of the bit patterns we ourselves have set aside for other types. To check that, we mask out all of the bits except for our set of quiet NaN bits. If all of those bits are set, it must be a NaN-boxed value of some other Lox type. Otherwise, it is actually a number.
The set of quiet NaN bits are declared like this:
#ifdef NAN_BOXING
#define QNAN ((uint64_t)0x7ffc000000000000)
typedef uint64_t Value;
It would be nice if C supported binary literals. But if you do the conversion, you’ll see that value is the same as this:

This is exactly all of the exponent bits, plus the quiet NaN bit, plus one extra to dodge that Intel value.
30 . 3 . 4Nil, true, and false
The next type to handle is nil. That’s pretty simple since there’s only one
nil value and thus we need only a single bit pattern to represent it. There
are two other singleton values, the two Booleans, true and false. This calls
for three total unique bit patterns.
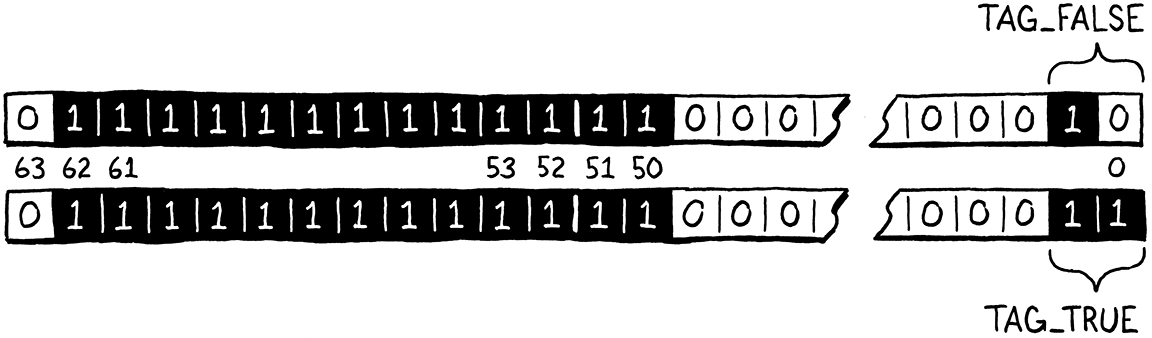
Two bits give us four different combinations, which is plenty. We claim the two lowest bits of our unused mantissa space as a “type tag” to determine which of these three singleton values we’re looking at. The three type tags are defined like so:
#define QNAN ((uint64_t)0x7ffc000000000000)
#define TAG_NIL 1 // 01. #define TAG_FALSE 2 // 10. #define TAG_TRUE 3 // 11.
typedef uint64_t Value;
Our representation of nil is thus all of the bits required to define our
quiet NaN representation along with the nil type tag bits:
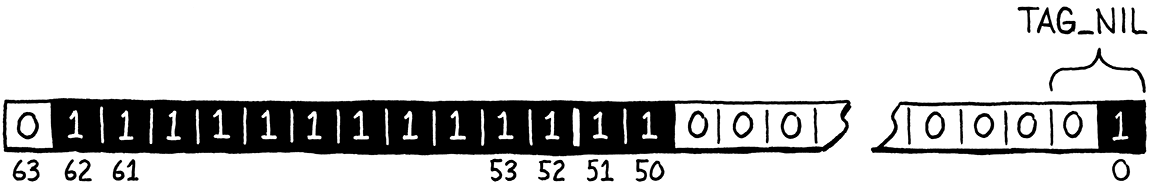
In code, we check the bits like so:
#define AS_NUMBER(value) valueToNum(value)
#define NIL_VAL ((Value)(uint64_t)(QNAN | TAG_NIL))
#define NUMBER_VAL(num) numToValue(num)
We simply bitwise OR the quiet NaN bits and the type tag, and then do a little cast dance to teach the C compiler what we want those bits to mean.
Since nil has only a single bit representation, we can use equality on
uint64_t to see if a Value is nil.
typedef uint64_t Value;
#define IS_NIL(value) ((value) == NIL_VAL)
#define IS_NUMBER(value) (((value) & QNAN) != QNAN)
You can guess how we define the true and false values.
#define AS_NUMBER(value) valueToNum(value)
#define FALSE_VAL ((Value)(uint64_t)(QNAN | TAG_FALSE)) #define TRUE_VAL ((Value)(uint64_t)(QNAN | TAG_TRUE))
#define NIL_VAL ((Value)(uint64_t)(QNAN | TAG_NIL))
The bits look like this:
To convert a C bool into a Lox Boolean, we rely on these two singleton values and the good old conditional operator.
#define AS_NUMBER(value) valueToNum(value)
#define BOOL_VAL(b) ((b) ? TRUE_VAL : FALSE_VAL)
#define FALSE_VAL ((Value)(uint64_t)(QNAN | TAG_FALSE))
There’s probably a cleverer bitwise way to do this, but my hunch is that the compiler can figure one out faster than I can. Going the other direction is simpler.
#define IS_NUMBER(value) (((value) & QNAN) != QNAN)
#define AS_BOOL(value) ((value) == TRUE_VAL)
#define AS_NUMBER(value) valueToNum(value)
Since we know there are exactly two Boolean bit representations in Lox—unlike
in C where any non-zero value can be considered “true”—if it ain’t true, it
must be false. This macro does assume you call it only on a Value that you
know is a Lox Boolean. To check that, there’s one more macro.
typedef uint64_t Value;
#define IS_BOOL(value) (((value) | 1) == TRUE_VAL)
#define IS_NIL(value) ((value) == NIL_VAL)
That looks a little strange. A more obvious macro would look like this:
#define IS_BOOL(v) ((v) == TRUE_VAL || (v) == FALSE_VAL)
Unfortunately, that’s not safe. The expansion mentions v twice, which means if
that expression has any side effects, they will be executed twice. We could have
the macro call out to a separate function, but, ugh, what a chore.
Instead, we bitwise OR a 1 onto the value to merge the only two valid Boolean bit patterns. That leaves three potential states the value can be in:
-
It was
FALSE_VALand has now been converted toTRUE_VAL. -
It was
TRUE_VALand the| 1did nothing and it’s stillTRUE_VAL. -
It’s some other, non-Boolean value.
At that point, we can simply compare the result to TRUE_VAL to see if we’re
in the first two states or the third.
30 . 3 . 5Objects
The last value type is the hardest. Unlike the singleton values, there are billions of different pointer values we need to box inside a NaN. This means we need both some kind of tag to indicate that these particular NaNs are Obj pointers, and room for the addresses themselves.
The tag bits we used for the singleton values are in the region where I decided to store the pointer itself, so we can’t easily use a different bit there to indicate that the value is an object reference. However, there is another bit we aren’t using. Since all our NaN values are not numbers—it’s right there in the name—the sign bit isn’t used for anything. We’ll go ahead and use that as the type tag for objects. If one of our quiet NaNs has its sign bit set, then it’s an Obj pointer. Otherwise, it must be one of the previous singleton values.
If the sign bit is set, then the remaining low bits store the pointer to the Obj:
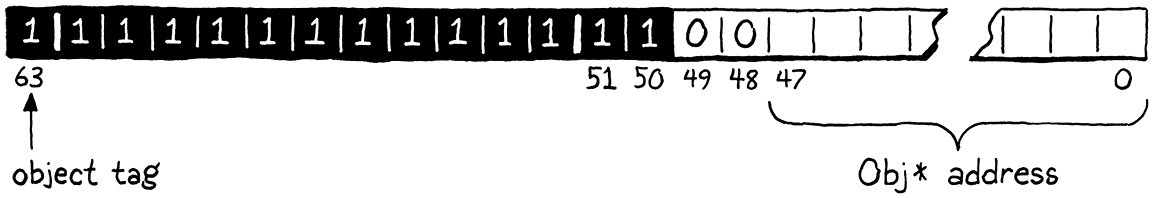
To convert a raw Obj pointer to a Value, we take the pointer and set all of the quiet NaN bits and the sign bit.
#define NUMBER_VAL(num) numToValue(num)
#define OBJ_VAL(obj) \ (Value)(SIGN_BIT | QNAN | (uint64_t)(uintptr_t)(obj))
static inline double valueToNum(Value value) {
The pointer itself is a full 64 bits, and in principle, it could thus overlap with some of those quiet NaN and sign bits. But in practice, at least on the architectures I’ve tested, everything above the 48th bit in a pointer is always zero. There’s a lot of casting going on here, which I’ve found is necessary to satisfy some of the pickiest C compilers, but the end result is just jamming some bits together.
We define the sign bit like so:
#ifdef NAN_BOXING
#define SIGN_BIT ((uint64_t)0x8000000000000000)
#define QNAN ((uint64_t)0x7ffc000000000000)
To get the Obj pointer back out, we simply mask off all of those extra bits.
#define AS_NUMBER(value) valueToNum(value)
#define AS_OBJ(value) \ ((Obj*)(uintptr_t)((value) & ~(SIGN_BIT | QNAN)))
#define BOOL_VAL(b) ((b) ? TRUE_VAL : FALSE_VAL)
The tilde (~), if you haven’t done enough bit manipulation to encounter it
before, is bitwise NOT. It toggles all ones and
zeroes in its operand. By masking the value with the bitwise negation of the
quiet NaN and sign bits, we clear those bits and let the pointer bits remain.
One last macro:
#define IS_NUMBER(value) (((value) & QNAN) != QNAN)
#define IS_OBJ(value) \ (((value) & (QNAN | SIGN_BIT)) == (QNAN | SIGN_BIT))
#define AS_BOOL(value) ((value) == TRUE_VAL)
A Value storing an Obj pointer has its sign bit set, but so does any negative number. To tell if a Value is an Obj pointer, we need to check that both the sign bit and all of the quiet NaN bits are set. This is similar to how we detect the type of the singleton values, except this time we use the sign bit as the tag.
30 . 3 . 6Value functions
The rest of the VM usually goes through the macros when working with Values, so we are almost done. However, there are a couple of functions in the “value” module that peek inside the otherwise black box of Value and work with its encoding directly. We need to fix those too.
The first is printValue(). It has separate code for each value type. We no
longer have an explicit type enum we can switch on, so instead we use a series
of type tests to handle each kind of value.
void printValue(Value value) {
in printValue()
#ifdef NAN_BOXING if (IS_BOOL(value)) { printf(AS_BOOL(value) ? "true" : "false"); } else if (IS_NIL(value)) { printf("nil"); } else if (IS_NUMBER(value)) { printf("%g", AS_NUMBER(value)); } else if (IS_OBJ(value)) { printObject(value); } #else
switch (value.type) {
This is technically a tiny bit slower than a switch, but compared to the overhead of actually writing to a stream, it’s negligible.
We still support the original tagged union representation, so we keep the old
code and enclose it in the #else conditional section.
}
in printValue()
#endif
}
The other operation is testing two values for equality.
bool valuesEqual(Value a, Value b) {
in valuesEqual()
#ifdef NAN_BOXING return a == b; #else
if (a.type != b.type) return false;
It doesn’t get much simpler than that! If the two bit representations are identical, the values are equal. That does the right thing for the singleton values since each has a unique bit representation and they are only equal to themselves. It also does the right thing for Obj pointers, since objects use identity for equality—two Obj references are equal only if they point to the exact same object.
It’s mostly correct for numbers too. Most floating-point numbers with different bit representations are distinct numeric values. Alas, IEEE 754 contains a pothole to trip us up. For reasons that aren’t entirely clear to me, the spec mandates that NaN values are not equal to themselves. This isn’t a problem for the special quiet NaNs that we are using for our own purposes. But it’s possible to produce a “real” arithmetic NaN in Lox, and if we want to correctly implement IEEE 754 numbers, then the resulting value is not supposed to be equal to itself. More concretely:
var nan = 0/0; print nan == nan;
IEEE 754 says this program is supposed to print “false”. It does the right thing
with our old tagged union representation because the VAL_NUMBER case applies
== to two values that the C compiler knows are doubles. Thus the compiler
generates the right CPU instruction to perform an IEEE floating-point equality.
Our new representation breaks that by defining Value to be a uint64_t. If we want to be fully compliant with IEEE 754, we need to handle this case.
#ifdef NAN_BOXING
in valuesEqual()
if (IS_NUMBER(a) && IS_NUMBER(b)) { return AS_NUMBER(a) == AS_NUMBER(b); }
return a == b;
I know, it’s weird. And there is a performance cost to doing this type test every time we check two Lox values for equality. If we are willing to sacrifice a little compatibility—who really cares if NaN is not equal to itself?—we could leave this off. I’ll leave it up to you to decide how pedantic you want to be.
Finally, we close the conditional compilation section around the old implementation.
}
in valuesEqual()
#endif
}
And that’s it. This optimization is complete, as is our clox virtual machine. That was the last line of new code in the book.
30 . 3 . 7Evaluating performance
The code is done, but we still need to figure out if we actually made anything better with these changes. Evaluating an optimization like this is very different from the previous one. There, we had a clear hotspot visible in the profiler. We fixed that part of the code and could instantly see the hotspot get faster.
The effects of changing the value representation are more diffused. The macros are expanded in place wherever they are used, so the performance changes are spread across the codebase in a way that’s hard for many profilers to track well, especially in an optimized build.
We also can’t easily reason about the effects of our change. We’ve made values smaller, which reduces cache misses all across the VM. But the actual real-world performance effect of that change is highly dependent on the memory use of the Lox program being run. A tiny Lox microbenchmark may not have enough values scattered around in memory for the effect to be noticeable, and even things like the addresses handed out to us by the C memory allocator can impact the results.
If we did our job right, basically everything gets a little faster, especially on larger, more complex Lox programs. But it is possible that the extra bitwise operations we do when NaN-boxing values nullify the gains from the better memory use. Doing performance work like this is unnerving because you can’t easily prove that you’ve made the VM better. You can’t point to a single surgically targeted microbenchmark and say, “There, see?”
Instead, what we really need is a suite of larger benchmarks. Ideally, they would be distilled from real-world applications—not that such a thing exists for a toy language like Lox. Then we can measure the aggregate performance changes across all of those. I did my best to cobble together a handful of larger Lox programs. On my machine, the new value representation seems to make everything roughly 10% faster across the board.
That’s not a huge improvement, especially compared to the profound effect of making hash table lookups faster. I added this optimization in large part because it’s a good example of a certain kind of performance work you may experience, and honestly, because I think it’s technically really cool. It might not be the first thing I would reach for if I were seriously trying to make clox faster. There is probably other, lower-hanging fruit.
But, if you find yourself working on a program where all of the easy wins have been taken, then at some point you may want to think about tuning your value representation. I hope this chapter has shined a light on some of the options you have in that area.
30 . 4Where to Next
We’ll stop here with the Lox language and our two interpreters. We could tinker on it forever, adding new language features and clever speed improvements. But, for this book, I think we’ve reached a natural place to call our work complete. I won’t rehash everything we’ve learned in the past many pages. You were there with me and you remember. Instead, I’d like to take a minute to talk about where you might go from here. What is the next step in your programming language journey?
Most of you probably won’t spend a significant part of your career working in compilers or interpreters. It’s a pretty small slice of the computer science academia pie, and an even smaller segment of software engineering in industry. That’s OK. Even if you never work on a compiler again in your life, you will certainly use one, and I hope this book has equipped you with a better understanding of how the programming languages you use are designed and implemented.
You have also learned a handful of important, fundamental data structures and gotten some practice doing low-level profiling and optimization work. That kind of expertise is helpful no matter what domain you program in.
I also hope I gave you a new way of looking at and solving problems. Even if you never work on a language again, you may be surprised to discover how many programming problems can be seen as language-like. Maybe that report generator you need to write can be modeled as a series of stack-based “instructions” that the generator “executes”. That user interface you need to render looks an awful lot like traversing an AST.
If you do want to go further down the programming language rabbit hole, here are some suggestions for which branches in the tunnel to explore:
-
Our simple, single-pass bytecode compiler pushed us towards mostly runtime optimization. In a mature language implementation, compile-time optimization is generally more important, and the field of compiler optimizations is incredibly rich. Grab a classic compilers book, and rebuild the front end of clox or jlox to be a sophisticated compilation pipeline with some interesting intermediate representations and optimization passes.
Dynamic typing will place some restrictions on how far you can go, but there is still a lot you can do. Or maybe you want to take a big leap and add static types and a type checker to Lox. That will certainly give your front end a lot more to chew on.
-
In this book, I aim to be correct, but not particularly rigorous. My goal is mostly to give you an intuition and a feel for doing language work. If you like more precision, then the whole world of programming language academia is waiting for you. Languages and compilers have been studied formally since before we even had computers, so there is no shortage of books and papers on parser theory, type systems, semantics, and formal logic. Going down this path will also teach you how to read CS papers, which is a valuable skill in its own right.
-
Or, if you just really enjoy hacking on and making languages, you can take Lox and turn it into your own plaything. Change the syntax to something that delights your eye. Add missing features or remove ones you don’t like. Jam new optimizations in there.
Eventually you may get to a point where you have something you think others could use as well. That gets you into the very distinct world of programming language popularity. Expect to spend a ton of time writing documentation, example programs, tools, and useful libraries. The field is crowded with languages vying for users. To thrive in that space you’ll have to put on your marketing hat and sell. Not everyone enjoys that kind of public-facing work, but if you do, it can be incredibly gratifying to see people use your language to express themselves.
Or maybe this book has satisfied your craving and you’ll stop here. Whichever way you go, or don’t go, there is one lesson I hope to lodge in your heart. Like I was, you may have initially been intimidated by programming languages. But in these chapters, you’ve seen that even really challenging material can be tackled by us mortals if we get our hands dirty and take it a step at a time. If you can handle compilers and interpreters, you can do anything you put your mind to.
Challenges
Assigning homework on the last day of school seems cruel but if you really want something to do during your summer vacation:
-
Fire up your profiler, run a couple of benchmarks, and look for other hotspots in the VM. Do you see anything in the runtime that you can improve?
-
Many strings in real-world user programs are small, often only a character or two. This is less of a concern in clox because we intern strings, but most VMs don’t. For those that don’t, heap allocating a tiny character array for each of those little strings and then representing the value as a pointer to that array is wasteful. Often, the pointer is larger than the string’s characters. A classic trick is to have a separate value representation for small strings that stores the characters inline in the value.
Starting from clox’s original tagged union representation, implement that optimization. Write a couple of relevant benchmarks and see if it helps.
-
Reflect back on your experience with this book. What parts of it worked well for you? What didn’t? Was it easier for you to learn bottom-up or top-down? Did the illustrations help or distract? Did the analogies clarify or confuse?
The more you understand your personal learning style, the more effectively you can upload knowledge into your head. You can specifically target material that teaches you the way you learn best.